建立如图所示的空间直角坐标系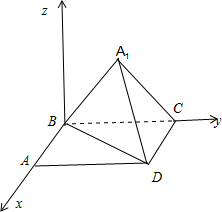，B（0，0，0），C（0，x，0），D（1，x，0）．

假设将△ABD沿矩形对角线BD所在的直线进行翻折时存在某个位置A₁BD，（A₁是点A翻折后的位置），使得AB⊥CD．

又∵BA₁⊥A₁D，∴BA₁⊥平面A₁CD．

设A₁（a，b，c），则

BA1

=（a，b，c），

CD

=(1，0，0)，

A1D

=（1-a，x-b，-c）．

由

BA1

•

A1D

=0，

BA1

•

CD

=0，得到

a(1-a)+b(x-b)-c2=0 a(1-a)=0

，得到

a=0 bx=b2+c2

或

a=1 bx=b2+c2

．

①当a=1时，此时矩形变为正方形，点A₁与C重合，满足AB⊥CD；

②当a=0时，点A₁位于yoz坐标平面内，此时，b²+c²=1，0＜b＜1，∴x=

1

b

＞1．

综上可知：当x≥1时，将△ABD沿矩形对角线BD所在的直线进行翻折，在翻折过程中，使得AB⊥CD．

故选C．