问题
解答题
在棱长为α的正方体ABCD- A1B1C1D1中,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点.
(1)求证:E、F、B、D四点共面;
(2)求证:平面AMN∥平面EFDB;
(3)求平面AMN和平面BFED间的距离.
答案
(1)证明: ,而E、F分别是
,而E、F分别是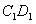 、
、 的中点,
的中点,
∴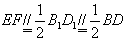 ,
,
∴E、F、B、D四点共面.
(2)证明:连结AC交BD于O点,连结A′C′,交MN、EF于G、K,
连结AG、OK,
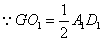 ,
,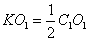 ,
,
∴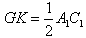 ,
,
又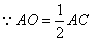 且
且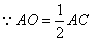 ,
,
∴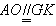 ,∴四边形AOKG为平行四边形 ,∴AG∥OK,
,∴四边形AOKG为平行四边形 ,∴AG∥OK,
∴AG∥平面BEFD,
又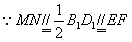 ,
,
∴MN∥平面BFED,
∴平面AMN∥平面BFED.
(3)解:过G作GH⊥OK于H,则GH即为所求,
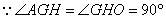 ,
,
∴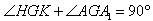 ,
,
又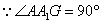 ,
,
∴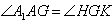 ,
,
又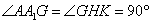 ,
,
∴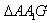 ∽△GHK,∴
∽△GHK,∴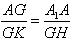 ,
,
又∵ ,∴
,∴ ,
,
又 ∵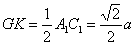 ,
,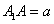 ,
,
∴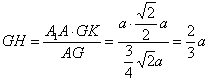 ,
,
所以,平面AMN与平面BFED之间距离为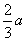 。
。

