问题
解答题
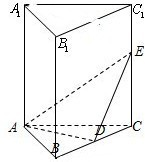
在直三棱柱ABC-A1B1C1中,D,E分别是棱BC,CC1上的点(点D异于B、C)且AD⊥DE.
(1)求证:面ADE⊥面BCC1B1
(2)若△ABC为正三角形,AB=2,AA1=4,E为CC1的中点,求二面角E-AD-C的正切值.
答案
(1)证明:∵三棱柱ABC-A1B1C1是直三棱柱,
∴CC1⊥平面ABC,
∵AD⊂平面ABC,
∴AD⊥CC1
又∵AD⊥DE,DE、CC1是平面BCC1B1内的相交直线
∴AD⊥平面BCC1B1,
∵AD⊂平面ADE
∴平面ADE⊥平面BCC1B1;
(2)由(1)知,AD⊥BC,
∵CC1⊥平面ABC,∴DE⊥AD,
∴∠EDC是二面角E-AD-C的平面角
∵△ABC为正三角形,AB=2,AA1=4,E为CC1的中点,
∴CD=1,CE=2
∴tan∠EDC=
=2.EC DC