问题
填空题
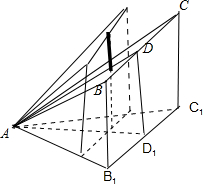
已知正△ABC的顶点A在平面α内，顶点B，C在平面α的同一侧，D为BC的中点，若△ABC在平面α内的射影是以A为直角顶点的三角形，则直线AD与平面α所成角的正弦值的最小值为______．
答案
如图所示，不妨设AB=2．则AD=
．3
假设一开始正△ABC在平面α内时的位置，则∠BAC=60°．
而当BC∥α时，其B、D、C三点的射影分别为B1，D1，C1时，且∠B1AC1=90°．
∠DAD1为直线AD与平面α所成角且最小．
则AD1=
B1C1=1 2
BC=1，∴DD1=1 2
=AD2-A D 21
．2
此时sin∠DAD1=
=DD1 AD
=2 3
．6 3
当BC与平面α部平行时，可以看出：其DD1长度必然增大．
因此直线AD与平面α所成角的正弦值的最小值为
．6 3
故答案为
．6 3
