问题
解答题
正数a,b,c满足a+b+c=1,求证:(1-a)(1-b)(1-c)≥8abc。
答案
见解析
证明:∵ a+b+c=1
∴ 1-a=b+c,1-b=a+c,1-c=a=b
∵ a>0,b>0,c>0
∴ b+c≥2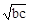 >0
>0
a+c≥2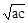 >0
>0
a+b≥2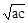 >0
>0
将上面三式相乘得:(b+c)(a+c)(a+b)≥8abc
即(1-a)(1-b)(1-c)≥8abc
正数a,b,c满足a+b+c=1,求证:(1-a)(1-b)(1-c)≥8abc。
见解析
证明:∵ a+b+c=1
∴ 1-a=b+c,1-b=a+c,1-c=a=b
∵ a>0,b>0,c>0
∴ b+c≥2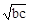 >0
>0
a+c≥2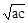 >0
>0
a+b≥2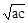 >0
>0
将上面三式相乘得:(b+c)(a+c)(a+b)≥8abc
即(1-a)(1-b)(1-c)≥8abc