问题
解答题
设数列{an}满足a1＝3，an＋1＝an2－2nan＋2，n＝1,2,3，…
(1)求a2，a3，a4的值，并猜想数列{an}的通项公式(不需证明)；
(2)记Sn为数列{an}的前n项和，试求使得Sn<2n成立的最小正整数n，并给出证明．
答案
（1）a2＝5，a3＝7，a4＝9，猜想an＝2n＋1
（2）Sn＝n2＋2n 见解析
解：(1)a2＝5，a3＝7，a4＝9，猜想an＝2n＋1.
(2)Sn＝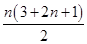
＝n2＋2n，
使得Sn<2n成立的最小正整数n＝6.
证明：n≥6(n∈N*)时都有2n>n2＋2n.
①n＝6时，26>62＋2×6，即64>48成立；
②假设n＝k(k≥6，k∈N*)时，2k>k2＋2k成立，那么2k＋1＝2·2k>2(k2＋2k)＝k2＋2k＋k2＋2k>k2＋2k＋3＋2k＝(k＋1)2＋2(k＋1)，即n＝k＋1时，不等式成立；
由①、②可得，对于所有的n≥6(n∈N*)
都有2n>n2＋2n成立．