答案：B

题目分析：当x=0时，显然无论a为何值，不等式|x|≥ax总恒成立；当x>0时，不等式|x|≥ax恒成立等价于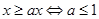：；当x<0时，不等式|x|≥ax恒成立等价于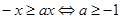：；所以对任意x∈R，不等式|x|≥ax恒成立，有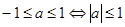；故选B．

另解：对任意x∈R，不等式|x|≥ax恒成立，等价于函数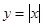的图象恒在直线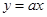的上方，如图：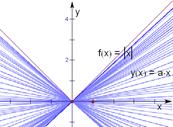

可知必须且只需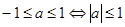；故选B．