问题
解答题
某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
答案
(1)100,50;(2)10.
题目分析:(1)方程的应用解题关键是设出未知数,找出等量关系,列出方程求解. 本题设乙队每天绿化x m2,则甲队每天绿化2x m2,等量关系为:在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(2)不等式的应用解题关键是找出不等量关系,列出不等式求解. 本题不等量关系为:这次的绿化总费用不超过8万元.
试题解析:(1)设乙队每天绿化x m2,则甲队每天绿化2x m2,
根据题意,得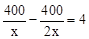 .
.
解得:x=50.
经检验,x=50.是原方程的根.
2x=100.
答:甲、乙两工程队每天能完成绿化的面积分别是100、50m2。
(2)设至少应安排甲队工作y天,则: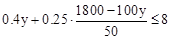 ,
,
解得y≥10.
答:至少应安排甲队工作10天.
