问题
选择题
在正项数列{an}中,若a1=1,且对所有n∈N*满足nan+1-(n+1)an=0,则a2014=( )
A.1011
B.1012
C.2013
D.2014
答案
答案:D
由a1=1,nan+1-(n+1)an=0可得 =
=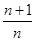 ,得到
,得到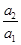 =
=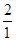 ,
,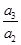 =
=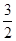 ,
,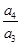 =
=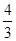 ,…,
,…, =
=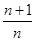 ,上述式子两边分别相乘得
,上述式子两边分别相乘得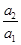 ×
×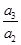 ×
×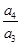 ×…×
×…× =an+1=
=an+1=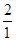 ×
×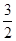 ×
×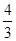 ×…×
×…×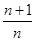 =n+1,故an=n,所以a2014=2014,故选D.
=n+1,故an=n,所以a2014=2014,故选D.
在正项数列{an}中,若a1=1,且对所有n∈N*满足nan+1-(n+1)an=0,则a2014=( )
A.1011
B.1012
C.2013
D.2014
答案:D
由a1=1,nan+1-(n+1)an=0可得 =
=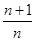 ,得到
,得到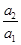 =
=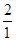 ,
,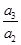 =
=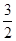 ,
,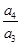 =
=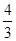 ,…,
,…, =
=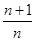 ,上述式子两边分别相乘得
,上述式子两边分别相乘得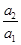 ×
×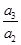 ×
×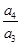 ×…×
×…× =an+1=
=an+1=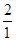 ×
×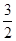 ×
×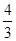 ×…×
×…×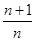 =n+1,故an=n,所以a2014=2014,故选D.
=n+1,故an=n,所以a2014=2014,故选D.