某校七年级准备购买一批笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,用360元钱购买的笔记本,打折后购买的数量比打折前多10本.
(1)求打折前每本笔记本的售价是多少元?
(2)由于考虑学生的需求不同,学校决定购买笔记本和笔袋共90件,笔袋每个原售价为6元,两种物品都打九折,若购买总金额不低于360元,且不超过365元,问有哪几种购买方案?
(1)4 (2)故有三种购买方案:
方案一:购买笔记本68本,购买笔袋22个;
方案二:购买笔记本69本,购买笔袋21个;
方案三:购买笔记本70本,购买笔袋20个;
思路分析:(1)设打折前售价为x,则打折后售价为0.9x,表示出打折前购买的数量及打折后购买的数量,再由打折后购买的数量比打折前多10本,可得出方程,解出即可;
(2)设购买笔记本y件,则购买笔袋(90-y)件,根据购买总金额不低于360元,且不超过365元,可得出不等式组,解出即可.
解:(1)设打折前售价为x,则打折后售价为0.9x,
由题意得,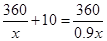 ,
,
解得:x=4,
经检验得:x=4是原方程的根,
答:打折前每本笔记本的售价为4元.
(2)设购买笔记本y件,则购买笔袋(90-y)件,
由题意得,360≤4×0.9×y+6×0.9×(90-y)≤365,
解得:67 ≤y≤70,
≤y≤70,
∵x为正整数,
∴x可取68,69,70,
故有三种购买方案:
方案一:购买笔记本68本,购买笔袋22个;
方案二:购买笔记本69本,购买笔袋21个;
方案三:购买笔记本70本,购买笔袋20个;
点评:本题考查了分式方程的应用、一元一次不等式组的应用,解答此类应用类题目,一定要先仔细审题,有时需要读上几遍,找到解题需要的等量关系或不等关系.
