为奖励“我的中国梦”暑期系列实践活动的获奖学生,学校准备在某商店购买A,B两种文具作为奖品,已知一件A种文具的单价比B种文具的单价便宜4元,而用300元买A种文具的件数是用200元买B种文具的件数的2倍.
(1)求A种文具的单价;
(2)根据需要,学校准备在该商店购买A,B两种文具共200件,其中A种文具的件数不多于B种文具件数的3倍.为了节约经费,应购买A,B两种文具各多少件?使用经费最少为多少元?
(1)12元;(2)应购进A种商品150件,B种商品50件,此时使用经费最少为2600元.
题目分析:(1)设A种文具的单价为x元,则B种文具的单价为每件(x+4)元,利用用300元买A种文具的件数是用200元买B种文具的件数的2倍得出等式,求出即可;
(2)设A种商品购进a件,则B种商品购进(200-a)件,根据“A种商品的件数不多于B种商品件数的3倍”列出不等式即可求得结果.
试题解析::(1)A种文具的单价为x元,则B种文具的单价为每件(x+4)元,
根据题意得出: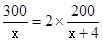 ,
,
解得:x=12,
经检验得出:x=12是原方程的根,
答:A种文具的单价为12元;
(2)设A种商品购进a件,则B种商品购进(200-a)件.
依题意,得0≤a≤3(200-a),
解得:0≤a≤150,
设所获利润为w元,则有
w=12a+16(200-a)=-4a+3200.
∵-4<0,
∴w随a的增大而减小.
∴当a=150时,所使用经费最少,
W最大=-4×150+3200=2600(元).
B文具为:200-150=50(件).
答:应购进A种商品150件,B种商品50件,此时使用经费最少为2600元.
