问题
选择题
数列1,1＋2,1＋2＋4，…，1＋2＋22＋…＋2n－1，…的前n项和Sn>1020，那么n的最小值是( )
A．7
B．8
C．9
D．10
答案
答案：D
∵1＋2＋22＋…＋2n－1＝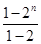
＝2n－1，
∴Sn＝(2＋22＋…＋2n)－n＝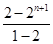
－n＝2n＋1－2－n.
若Sn>1020，则2n＋1－2－n>1020，∴n≥10.
故选D项．
搜题请搜索小程序“爱下问搜题”
数列1,1＋2,1＋2＋4，…，1＋2＋22＋…＋2n－1，…的前n项和Sn>1020，那么n的最小值是( )
A．7
B．8
C．9
D．10
答案：D
∵1＋2＋22＋…＋2n－1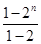＝＝2n－1，
∴Sn＝(2＋22＋…＋2n)－n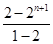＝－n＝2n＋1－2－n.
若Sn>1020，则2n＋1－2－n>1020，∴n≥10.
故选D项．