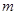（1）的取值范围（2）的取值范围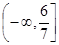

题目分析:（1）对于含二次项恒成立的问题，注意讨论二次项系数是否为0，这是学生容易漏掉的地方.（2）恒成立问题一般需转化为最值，利用单调性证明在闭区间的单调性.（3）一元二次不等式在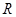上恒成立，看开口方向和判别式.（4）含参数的一元二次不等式在某区间内恒成立的问题通常有两种处理方法：一是利用二次函数在区间上的最值来处理；二是分离参数，再去求函数的最值来处理，一般后者比较简单.

试题解析:解析（1）由题意可得m＝0或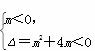⇔m＝0或－4＜m＜0

⇔－4＜m≤0.

故m的取值范围为(－4,0].                               6分

（2）∵f(x)＜－m＋5⇔m(x²－x＋1)＜6，

∵x²－x＋1＞0，∴m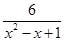＜对于x∈[1,3]恒成立，

记g(x)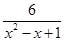＝，x∈[1,3]，

记h(x)＝x²－x＋1，h(x)在x∈[1,3]上为增函数.则g(x)在[1,3]上为减函数，  

∴[g(x)]_min＝g（3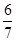）＝，  ∴m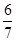＜.   所以m的取值范围为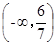.      3分