问题
填空题
某人从A地向北偏东30°走了20米到达B地，又从B地向南偏东30°走了20米到达C地，此时C地在A地的______方向．
答案
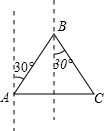
∵AB=BC，∠ABC=30°+30°=60°
∴△ABC是等边三角形．
∴∠BAC=60°
∴∠DAC=90°
∴DA⊥AC
即C地在A地的正东方向．
搜题请搜索小程序“爱下问搜题”
某人从A地向北偏东30°走了20米到达B地，又从B地向南偏东30°走了20米到达C地，此时C地在A地的______方向．
∵AB=BC，∠ABC=30°+30°=60°
∴△ABC是等边三角形．
∴∠BAC=60°
∴∠DAC=90°
∴DA⊥AC
即C地在A地的正东方向．