问题
填空题
函数f(x)＝－x3＋mx2＋1(m≠0)在(0,2)内的极大值为最大值，则m的取值范围是________．
答案
(0,3)
f′(x)＝－3x2＋2mx＝x(－3x＋2m)．
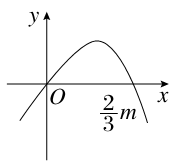
令f′(x)＝0，得x＝0或x＝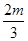
.
∵x∈(0,2)，∴0<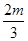<2，
∴0<m<3.
搜题请搜索小程序“爱下问搜题”
函数f(x)＝－x3＋mx2＋1(m≠0)在(0,2)内的极大值为最大值，则m的取值范围是________．
(0,3)
f′(x)＝－3x2＋2mx＝x(－3x＋2m)．
令f′(x)＝0，得x＝0或x＝.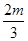
∵x∈(0,2)，∴0<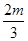<2，
∴0<m<3.