问题
解答题
已知曲线C:y=x3-3x2,直线l:y=-2x
(1)求曲线C与直线l围成的区域的面积;
(2)求曲线y=x3-3x2(0≤x≤1)与直线l围成的图形绕x轴旋转一周所得的旋转体的体积.
答案
(1)联立y=x3-3x2与y=-2x得:x=0,1或2.
∴曲线C与直线l有三个交点.
y'=3x2-6x令y′=0得:x=0或x=2
∵当x∈(-∞,0)∪(2,+∞)时,
y′>0,当x∈(0,2)时,y'<0,
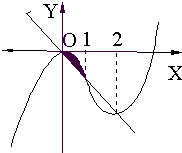
∴曲线C大致形状如图所示.
∴S=∫
[x3-3x2-(-2x)]dx+∫1 0
(-2x-x3+3x2)dx=2 1 1 2
(2)由题意,旋转体的体积V=∫
π[(-2x)2-(x3-3x2)2]dx=1 0
π41 105