问题
计算题
一辆长为l1 =" 14" m的客车沿平直公路以v1 =" 8" m/s的速度匀速向东行驶，一辆长为l2 =" 10" m的货车由静止开始以a =" 2" m/s2的加速度由东向西匀加速行驶，已知货车刚启动时两车前端相距s0 =" 240" m，当货车的速度达到v2 =" 24" m/s时即保持该速度匀速行驶，求两车错车所用的时间。
答案
0.75 s
由已知客车长l ＝ 14 m，它做匀速运动，v客＝ 8 m/s
货车长d ＝ 10 m，加速度为a ＝ 2 m/s，两车开始相距s0 ＝ 240 m，设经过t1时间两车车头相遇，并设想火车始终在做匀加速运动
则 v客·t1 ＋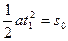
可得 t1＝12 s （4分）
此时货车的行驶速度为：
v货＝a t1 ＝ 24 m/s （火车恰好达到最大速度，设想成立）（4分）
设错车时间为t2，则两车错车时刚好匀速错车
则 v客·t2 ＋v货·t2 ＝l1+ l2 （4分）
可得 t2 =" 0.75" s （4分）
方法二：设经过t1时间货车速度达到v2，则：
t1 = v2/a =" 12" s （4分）
在t1时间内，两车位移分别为：
x1 = v1 t1 =" 96" m x2 =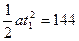 
m ∵x1 + x2 =" 240" m = s0
说明此时两车刚好前端相遇，则两车错车时刚好匀速错车（4分）
设错车时间为t2，则：
v1·t2 ＋v2·t2 ＝l1+ l2 （4分）
可得 t2 =" 0.75" s （4分）