S=∫_-21(9-x2-x-7)将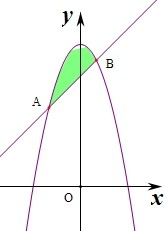y=x+7代入y=9-x²，

得x+7=9-x²，

即x²+x-2=0，

解得x=1或x=-2，

∴由积分的几何意义可知封闭区域的面积S=

∫

1-2

(9-x2-x-7)dx=（-

1

3

x3-

1

2

x2+2x）|

1-2

=（-

1

3

-

1

2

+2）-（

1

3

×8-

1

2

×4-2×2）=

9

2

．

故答案为：

9

2