问题
填空题
曲线y=x2，x=0，y=1，所围成的图形的面积可用定积分表示为______．
答案
作出对应的图形如图：
则两个图象的交点横坐标分别为0和1，
∴根据积分的几何意义可知，所围成的图形的面积可用定积分表示为：
（1-x2）dx．∫ 10
故答案为：
（1-x2）dx．∫ 10
搜题请搜索小程序“爱下问搜题”
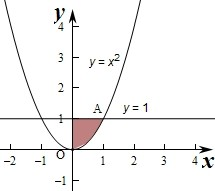
曲线y=x2，x=0，y=1，所围成的图形的面积可用定积分表示为______．
作出对应的图形如图：
则两个图象的交点横坐标分别为0和1，
∴根据积分的几何意义可知，所围成的图形的面积可用定积分表示为：
（1-x2）dx．∫ 10
故答案为：
（1-x2）dx．∫ 10