问题
填空题
已知f(x)=|lg(x-2)|,当a<b时,f(a)=f(b),则a+b的取值范围为______.
答案
∵f(x)=|lg(x-2)|,其图象如图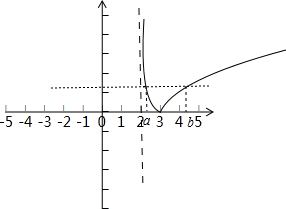
∵f(a)=f(b),
∴a,b为方程f(x)=m (m>0)的两个根,又∵a<b,由图可知2<a<3,b>3
∴|lg(a-2)|=|lg(b-2)|,
即-lg(a-2)=lg(b-2)
即(a-2)(b-2)=1
∵1=(a-2)(b-2)≤(
)2=(a-2)+(b-2) 2 (a+b-4)2 4
∴a+b-4≥2或a+b-4≤-2(舍去)
∴a+b≥6
故答案为 (6,+∞)
