问题
问答题
如图1所示的电路中,AB是一段粗细均匀的电阻丝,R是保护电阻,电阻值为2Ω,电源的电动势为6V,安培表内阻为零,其示数为I,滑动片P与电阻丝有良好的接触,且AP长为L,其它连接导线电阻不计.闭合电键,调节P的位置,记录L和与之相对应的I数据,并同时计算出
值列表如下:1 I
| 实验次数 | 1 | 2 | 3 | 4 | 5 | ||
| L(m) | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | ||
| I(A) | 1.78 | 1.39 | 1.09 | 0.96 | 0.83 | ||
| 0.56 | 0.72 | 0.92 | 1.04 | 1.20 |
| 1 |
| I |
(2)从
-L的图象中求出截距b和斜率k1 I
(3)根据截距和斜率,求出电源内电阻r和该电阻丝单位长度电阻R0
答案
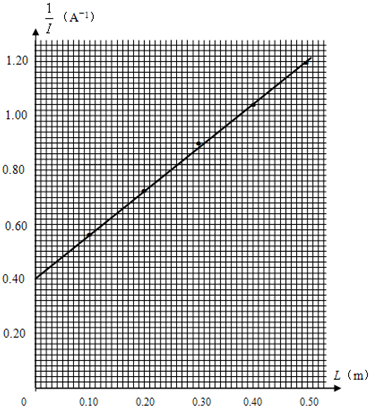
(1)应用描点法作图,图象如图所示.
(2)由图象可知,图象的截距b=0.38,图象的斜率k═
=△ 1 i △L
=1.575;1.14-0.51 0.50-0.10
电阻线接入电路的阻值R线=R0L,由闭合电路的欧姆定律可得:
(3)由闭合电路的欧姆定律得,电路电流i=
,则E r+R0L+R
=1 i
+r+R E
L;R0 E
由图象可得:b=
=0.38,k=r+R E
=R0 E
=△ 1 i △L
=1.575,1.14-0.51 0.50-0.10
R=2Ω,E=6V,解得:r=0.28Ω,R0=9.45Ω.
故答案为:(1)图象如图所示;(2)截距b=0.38(0.38-0.42均正确),
斜率k=1.575(1.56-1.64均正确);
(3)r=0.28(0.28-0.52均正确)Ω;R0=9.45(9.36-9.84均正确)Ω.