问题
解答题
已知函数f(x)=ax-lnx
(I)当a=1时,求f(x)的最小值;
(Ⅱ)当a>0时,求f(x)在[1,e]上的最大值与最小值.
答案
(I)当a=1时,f(x)=x-lnx(x>0),
f′(x)=1-
=1 x
.x-1 x
当x∈(0,1)时,f′(x)<0,f(x)单调递减.
当x∈(1,+∞)时,f′(x)>0,f(x)单调递增.
所以当x=1时f(x)取得极小值,也是最小值为f(1)=1.
(II)由f(x)=ax-lnx(x>0).
则f′(x)=a-
=1 x
.ax-1 x
由f′(x)>0,得x>
,由f′(x)<0,得0<x<1 a
.1 a
所以f(x)在(0,
)上为减函数,在(1 a
,+∞)上为增函数.1 a
当0<a≤
时,fmin=f(e)=ae-1,1 e
=f(1)=a.f max
当
<a≤1 e
时,fmin=f(1 e-1
)=1+lna,1 a
=f(1)=a.f max
当
<a<1时,fmin=f(1 e-1
)=1+lna,1 a
=f(e)=ae-1.f max
当a≥1时,fmin=f(1)=a,
=f(e)=ae-1.f max

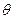 角时,小球的速率为 ( )
角时,小球的速率为 ( )