问题
填空题
已知a∈(0，＋∞)，函数f(x)＝ax2＋2ax＋1，若f(m)<0，比较大小：f(m＋2)________1(用“<”“＝”或“>”连接)．
答案
>
由f(x)＝ax2＋2ax＋1(a>0)知f(x)过定点(0,1)．又f(x)＝ax2＋2ax＋1＝a(x＋1)2－a＋1(a>0)，设f(x)＝0的两个实数根为x1，x2，且x1<x2，如图所示．所以x1＋x2＝－2，x1x2＝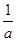
，由Δ>0得a>1，所以x2－x1＝
＝
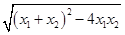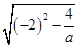∈(0,2)．
又因为对称轴为直线x＝－1，f(0)＝1，
所以x2∈(－1,0)．
由f(m)<0，得x1<m<x2，
所以m＋2>0，所以f(m＋2)>1.
