（Ⅰ）因为f′（x）=（x²-3x+3）•e^x+（2x-3）•e^x=x（x-1）•e^x．

当t＞1时，由f′（x）＞0，可得t＞x＞1或-2＜x＜0；由f′（x）＜0，可得0＜x＜1

所以f（x）在（-2，0），（1，t）上递增，在（0，1）上递减．

（Ⅱ）证明：由f′（x）＞0，可得x＞1或x＜0；由f′（x）＜0，可得0＜x＜1

所以f（x）在（-∞，0），（1，+∞）上递增，在（0，1）上递减，所以f（x）在x=1处取得极小值f（1）=e．

又∵f（-2）=13e^-2＜e，所以f（x）仅在x=-2处取得[-2，t]上的最小值f（-2）

从而当t＞-2时，f（-2）＜f（t），即m＜n．

（Ⅲ）设g（x）=f（x）+（x-2）e^x=（x-1）²e^x，当x＞1时判断方程g（x）=x根的个数等价于（x-1）²e^x=x当x＞1时根的个数

设h（x）=（x-1）²e^x-x（x＞1），则h′（x）=（x²-1）e^x-1，

再设k（x）（x²-1）e^x-1（x＞1），则k′（x）=（x²+2x-1）e^x，

当x＞1时，k′（x）＞1，即k（x）在（1，+∞）单调递增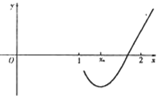

∵k（1）=-1＜0，k（2）=3e²-1＞0

∴在（1，2）上存在唯一x₀，使k（x₀）=0，即存在唯一x₀∈（1，2），使h′（x₀）=0

函数h（x）在（1，x₀）上，h′（x₀）＜0，函数单调减，在（x₀，+∞）上，h′（x₀）＞0，函数单调增，

∴h（x）_min=h（x₀）＜h（1）=-1＜0

∵h（2）=e²-2＞0

y=h（x）的大致图象如图，

由此可得y=h（x）在（1，+∞）上只有一个零点，即g（x）=x，x＞1时只有1个实根．