问题
填空题
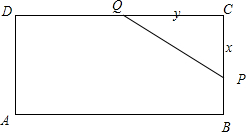
在矩形ABCD中,AB=5,BC=2,现截去一个角△PCQ,使P、Q分别落在边BC、CD上,且△PCQ的周长为8,设PC=x,CQ=y,则用x表示y的表达式为y=______.
答案
如图
由题意可得0≤x≤2,由勾股定理可得PQ=
,x2+y2
故△PCQ的周长=x+y+
=8,即x2+y2
=8-x-y,x2+y2
平方可得x2+y2=64+x2+y2-16x-16y+2xy,
整理可得32=8x+8y-xy,即(8-x)y=32-8x,
故y=
,(0≤x≤2)32-8x 8-x
故答案为:
,(0≤x≤2)32-8x 8-x