问题
解答题
某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买3000千克以上(含3000千克)的有两种销售方案.甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回.已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司的两种购买方案的付款y(元)与所购买的水果量x(千克)之间的函数关系式.
(2)当购买量在什么范围内时,选择哪种方案付款较少?说明理由.
答案
(1)y甲=9x(x≥3000),y乙=8x+5000(x≥3000).
(2)当y甲=y乙时,即9x=8x+5000,
解得x=5000.
∴当x=5000千克时,两种付款一样.
当y甲<y乙时,有
x≥3000 9x<8x+5000
解得3000≤x<5000.
∴当3000≤x<5000时,选择甲种方案付款少.
当y甲>y乙时,有x>5000,
∴当x>5000千克时,选择乙种方案付款少.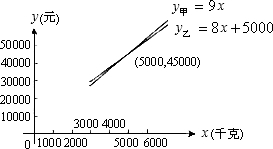
方法二:图象法
作出它们的函数图象(如图)
由函数图象可得,当购买量大于或等于3000千克且小于5000千克时,选择甲方案付款最少;
当购买量等于5000千克时,两种方案付款一样;
当购买量大于5000千克时,选择乙方案付款最少.

 V
V