问题
填空题
函数y＝lnx＋ax有两个零点，则a的取值范围是________．
答案
(－
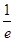，0)
因为函数y＝lnx＋ax，所以y′＝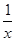
＋a，若函数存在两个零点，则必须a<0，令y′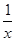＝＋a＝0得x0＝－
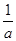.当0<x<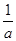－时，y′>0，函数单调递增；当x>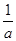－时，y′<0，函数单调递减，因为函数y＝lnx＋ax有两个零点，故ln
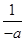－1>0，得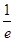－<a<0.
搜题请搜索小程序“爱下问搜题”
函数y＝lnx＋ax有两个零点，则a的取值范围是________．
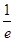(－，0)
因为函数y＝lnx＋ax，所以y′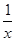＝＋a，若函数存在两个零点，则必须a<0，令y′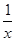＝＋a＝0得x0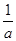＝－.当0<x<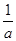－时，y′>0，函数单调递增；当x>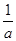－时，y′<0，函数单调递减，因为函数y＝lnx＋ax有两个零点，故ln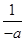－1>0，得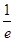－<a<0.