问题
计算题
(10分)甲、乙两车同时同向从同一地点出发，甲车以v1＝16 m/s的初速度，a1＝－2 m/s2的加速度做匀减速直线运动，乙车以v2＝4 m/s的初速度，a2＝1 m/s2的加速度做匀加速直线运动，求两车再次相遇前两车相距最大距离和再次相遇时两车运动的时间．
答案
8 s后两车再次相遇
由题意得v1＋a1t1＝v2＋a2t1
∴t1＝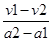
＝
s＝4 s
此时Δx＝x1－x2
＝(v1t1－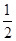
a1t2)－(v2t1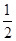＋a2t2)
＝[16×4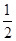＋×(－2)×42]m－(4×4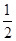＋×1×42) m
＝24 m
设经过时间t2，两车再次相遇，则
v1t2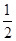＋a1t2＝v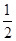2t2＋a2t2
解得t2＝0(舍)或t2＝8 s．
所以8 s后两车再次相遇
本题考查匀变速直线运动的追击相遇问题，速度相等是两车能追上或追不上的临界条件，由此判断出两车速度相等的时刻，分别求得该时刻的位移，进行比较发现在该时刻两车位移差值为24m，由此判断两车已经相遇一次，此后还有相遇的可能，根据位移相等继续判断，如果方程有正解，说明能够再次相遇