问题
解答题
甲,乙两辆汽车同时从同一地点A出发,沿同一方向直线行驶,每辆车最多只能带240L汽油,途中不能再加油,每升油可使一辆车前进12km,两车都必须沿原路返回出发点,但是两车相互可借用对方的油.请你设计一种方案,使其中一辆车尽可能地远离出发地点A,并求出这辆车一共行驶了多少千米?
答案
设尽可能远离A地的甲汽车共走了x千米,乙汽车共走了y千米,则
x+y≤240×12×2,且x-y≤240×12
∴x≤4320
所以x最大为4320千米.
设从A到尽可能的离A的距离是m千米,其中借给对方油的那辆车走了n千米后停下,
那么m=n+(240-x÷12×2)×12÷2=1440千米
那么需要用油1440÷12=120升,那么就是走这个最远距离一次(单趟)需要120升油,
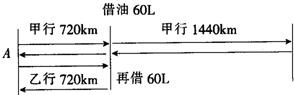
那么可得出的方案是:甲,乙共同走720千米,乙停下等甲,并且给甲60升汽油,甲再走1440千米后回头与乙会合,乙再给甲60升汽油后,两车同时回到A地.
也可画图表示为:(如右图).