问题
计算题
（14分）在一平直的公路上，甲车以2m/s2的加速度起动，此时乙车刚好以10m/s的速度匀速从甲车旁驶过，问：
（1）甲车追上乙车前，何时两车距离最远？最远距离是多少？
（2）甲车经多长时间追上乙车？
（3）甲车追上乙车后立即以恒定的加速度刹车，求乙车再次追上甲车时甲车的速度。
答案
（1）25m （2）t＝10s（3）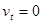
题目分析：（1）根据匀变速直线运动的规律可得甲车的速度为
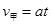…………1分
经分析，当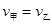
时，两车距离最远， …………1分
即
，解得：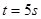
…………1分
由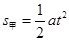
，
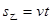得 …………2分
；
，
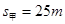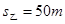最大距离为△S＝s乙－s甲＝25m …………1分
（2）当甲车追上乙车时满足位移关系s甲＝s乙，即：
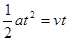…………2分
解得t＝10s …………2分
（3）当乙车追上甲车时，乙车与甲车在相同的时间内位移相同，因此平均速度相同，甲车的平均速度为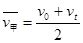
（其中v0＝at＝20m/s），乙车的平均速度
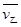即为乙车的速度为10m/s，由
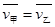可得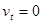。 …………（4分）
（其它方法正确合理亦可得满分）
点评：本题难度较小，两物体能否追上或相遇最远、最近的临界条件是两物体的速度相同，求解相遇问题关键要判断出位移和时间上的等量关系