问题
解答题
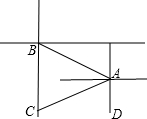
灯塔A在灯塔B的南偏东60°方向上,A、B相距30海里,轮船C在B的正南方向,在灯塔A的南偏西60°方向上,通过画图(用1个单位代表10海里)确定轮船C的位置,求∠BAC和∠ACB的度数,并求出轮船C与灯塔B的距离.
答案
如图,灯塔A在灯塔B的南偏东60°方向上,即∠CBA=60°,
A、B相距30海里,轮船C在B的正南方向,在灯塔A的南偏西60°方向上,即∠CAD=60°.
∵∠CAD与∠ACB是内错角,故∠CAD=∠ACB=60°,
在△ABC中∵∠CBA=60°,∠ACB=∠CAD=60°,
∴∠BAC=180°-∠CBA-∠ACB=180°-60°-60°=60°,即∠BAC=∠ACB=60°.
故△ABC是等边三角形,AB=BC=30,
即轮船C与灯塔B的距离是30海里.