问题
解答题
已知数列{an}的第一项a1=5且Sn-1=an(n≥2, n∈N*)。
(1)求a2,a3,a4,并由此猜想an的表达式;
(2)用数学归纳法证明{an}的通项公式。
答案
解:(1)a2=S1=a1=5,a3=S2=a1+a2=10,
a4=S3=a1+a2+a3=5+5+10=20,
猜想an=5×2n-2(n≥2,n∈N*);
(2)证明:①当n=2时,a2=5×22-2=5,猜想成立,
②假设n=k时成立,即ak=5×2k-2(k≥2,k∈N*),
当n=k+1时,由已知条件和假设有ak+1=Sk=a1+a2+…+ak=5+5+10+…+5×2k-2
故n=k+1时,猜想也成立,
由①②可知,对n≥2,n∈N*有an=5×2n-2,
所以数列{an}的通项an=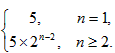 。
。
