虚数（x-2）+yi（x，y∈R）的模为

3

，即（x-2）²+y²=3

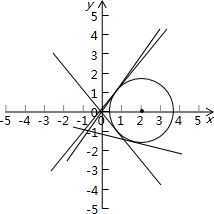
就是以（2，0）为圆心以

3

为半径的圆，

y

x

的几何意义点与原点连线的斜率，

易得

y

x

的最大值是：

3

y+1

x+1

的几何意义是圆上的点与（-1，-1）连线的斜率，求

y+1

x+1

的最小值

为：

y+1

x+1

=k，kx-y-1+k=0直线与圆相切时k最大和最小

3

=

|2k-1+k|

1+k2

解得k=

3- 21

6

时最大．

故答案为：

3

；

3- 21

6

．