z的共轭复数为4-3i或-4+3i

方法一 （3+4i)(a+bi)=(3a-4b)+(4a+3b)i是纯虚数，

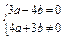∴,∴b=a,代入a²+b²=25,得a=±4.

∴a=4时，b=3;a=-4时，b=-3.

∴z=4+3i或z=-4-3i.

故所求的z的共轭复数为4-3i或-4+3i.

方法二 设(3+4i)（a+bi）=ki(k∈R，k≠0),

∴a+bi===,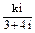

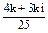∴a=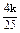,b=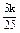,代入a²+b²=25,得k=±25.

∴k=25时，z=4+3i,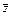=4-3i;

k=-25时，z="-4-3i," 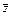=-4+3i.