解：（I）由AB、BC、AC为有理数及余弦定理知cosA=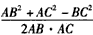是有理数；

（II）用数学归纳法证明cosnA和sinA·sinnA都是有理数

①当n=1时，由（I）知cosA是有理数，从而有sinA·sin A=1-cos2A也是有理数

②假设当n=k（k≥1）时，coskA和sinA·sinkA都是有理数

当n=k+1时，由cos（k+1）A=cosA·coskA-sinA·sinkA

sin A·sin（k+1）A=sin A·（sin A·coskA+cosA·sinkA）=（sinA·sin A）·coskA+（sinA·sinkA）·cosA，及①和归纳假设，知cos（k+1）A与sin A·sin（k+l）A都是有理数

即当n=k+1时，结论成立。

综合①、②可知，对任意正整数n，cosnA是有理数。