解：假设存在a、b、c使1²+2²+3²+…n²+（n﹣1）²+…2¹+1²=a_ⁿ（b^_n2+c）对于一切n∈N*都成立．当n=1时，a（b+c）=1；当n=2时，2a（4b+c）=6；当n=3时，3a（9b+c）=19．

解方程组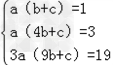，解得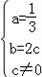

证明如下：

①当n=1时，由以上知存在常数a、b、c使等式成立．

②假设n=k（k∈N*）时等式成立，

即1²+2²+3²+…k²+（k﹣1）²+…2¹+1²=a_^k（b^_k2+c）=；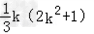

当n=k+1时，1²+2²+3²+…（k+1）²+k²+…2¹+1²=ak（bk²+c）

=+（k+1）²+k²=；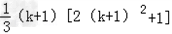

即n=k+1时，等式成立．

因此存在，使等式对一切n∈N*都成立．