问题
计算题
已知x的值满足式子x2+x﹣1=0，求2008x3+4016x2的值．
答案
解：∵x2+x﹣1=0，
∴由求根公式得：x=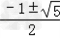
2008x3+4016x2=2008x2（x+2）
把x=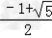
值代入得：2008x2（x+2）=2008×
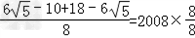=2008，
把x=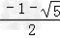
值代入得：2008x2（x+2）=2008×
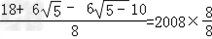=2008．
答：所求值为2008．
搜题请搜索小程序“爱下问搜题”
已知x的值满足式子x2+x﹣1=0，求2008x3+4016x2的值．
解：∵x2+x﹣1=0，
∴由求根公式得：x=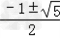
2008x3+4016x2=2008x2（x+2）
把x=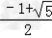值代入得：2008x2（x+2）=2008×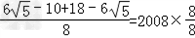=2008，
把x=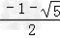值代入得：2008x2（x+2）=2008×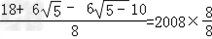=2008．
答：所求值为2008．