问题
计算题
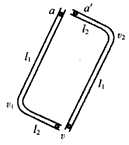
两支完全相同的光滑直角弯管,如图所示在竖直平面内放置,现有两只相同的小球a和a'同时从管口由静止滑下,问谁先从下端的出口掉出?
答案
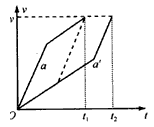
解:利用速率图像进行分析。根据拐角处的高低,首先可以确定小球到达拐角处的速率v1>v2,而两小球到达出口时的速率v相等。又由题意可知两球经历的总路程s相等,根据图中管的倾斜程度,小球a第一阶段的加速度跟小球a'第二阶段的加速度大小相同(设为a1);小球a第二阶段的加速度跟小球a'第一阶段的 加速度大小相同(设为a2),显然有a1>a2。根据这些物理量大小的分析,在同一个v-t图像(速率-时间图像)中两球速率曲线下所围的面积应该相同,且末状态速率也相同(纵坐标相同)。开始时,a球曲线的斜率大。由于两球两阶段加速度对应相等,如果同时到达(经历时间为t1)则必然有s1>s2,显然不合理。考虑到两球末状态速率相等(图中v),两球的速率图像只能如图所示。因此有t1<t2,即a球先从下端的出口掉出