问题
证明题
设函数f(x)对定义域内任意实数都有f(x)≠0,且f(x+y)=f(x)·f(y)成立。
求证:对定义域内任意x都有f(x)>0。
答案
证明:设对满足题设条件的任意x,f(x)>0不成立,即存在某个x0,使f(x0)≤0,
∵f(x)≠0,
∴f(x0)<0,
又知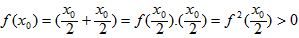
这与假设,f(x0)<0矛盾,所以假设不成立,
故对定义域内任意的x都有f(x)>0。
设函数f(x)对定义域内任意实数都有f(x)≠0,且f(x+y)=f(x)·f(y)成立。
求证:对定义域内任意x都有f(x)>0。
证明:设对满足题设条件的任意x,f(x)>0不成立,即存在某个x0,使f(x0)≤0,
∵f(x)≠0,
∴f(x0)<0,
又知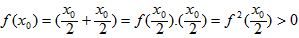
这与假设,f(x0)<0矛盾,所以假设不成立,
故对定义域内任意的x都有f(x)>0。