问题
证明题
设直线l1：y=k1x+1，l2：y=k2x-1，其中实数k1，k2满足k1k2+2=0，
(1)证明l1与l2相交；
(2)证明l1与l2的交点在椭圆2x2+y2=1上．
答案
证明：(1)反证法．假设l1与l2不相交，则l1与l2平行，有k1=k2，
代入k1k2+2=0，得k12+2=0，此与k1为实数的事实相矛盾，
从而k1≠k2，即l1与l2相交．
(2)由方程组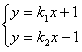
，解得交点P的坐标(x，y)为
，
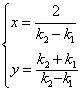而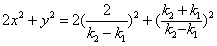
，
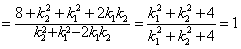此即表明交点P(x，y)在椭圆2x2+y2=1上．