问题
解答题
己知下 * * 个方程 x2+4ax-4a+3=0,x2+(a-1)x+a2=0,x2+2ax-2a=0至少有一个方程有实根,求实数a的取值范围.
答案
解:假设没有一个方程有实数根,
则:16a2﹣4(3﹣4a)<0(1)
(a﹣1)2﹣4a2<0(2)
4a2+8a<0(3)
解之得: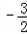 <a<﹣1
<a<﹣1
故三个方程至少有一个方程有实根的a的取值范围是:{a|a≥﹣1或a≤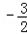 }.
}.
己知下 * * 个方程 x2+4ax-4a+3=0,x2+(a-1)x+a2=0,x2+2ax-2a=0至少有一个方程有实根,求实数a的取值范围.
解:假设没有一个方程有实数根,
则:16a2﹣4(3﹣4a)<0(1)
(a﹣1)2﹣4a2<0(2)
4a2+8a<0(3)
解之得: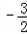 <a<﹣1
<a<﹣1
故三个方程至少有一个方程有实根的a的取值范围是:{a|a≥﹣1或a≤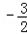 }.
}.