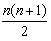观察下列等式:
(1+x+x2)1=1+x+x2,
(1+x+x2)2=1+2x+3x2+2x3+x4,
(1+x+x2)3=1+3x+6x2+7x3+6x4+3x5+x6,
(1+x+x2)4=1+4x+10x2+16x3+19x4+16x5+10x6+4x7+x8 ,
……
由以上等式推测:
对于n∈N*,若(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n,则a2=( )。
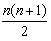
观察下列等式:
(1+x+x2)1=1+x+x2,
(1+x+x2)2=1+2x+3x2+2x3+x4,
(1+x+x2)3=1+3x+6x2+7x3+6x4+3x5+x6,
(1+x+x2)4=1+4x+10x2+16x3+19x4+16x5+10x6+4x7+x8 ,
……
由以上等式推测:
对于n∈N*,若(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n,则a2=( )。