问题
问答题
设A是三阶实对称阵,A~B,其中
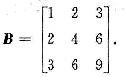
(Ⅰ)求A的特征值;
(Ⅱ)若A的对应于λ1=λ2=0的特征向量为ξ1=1,1,0T,ξ22,2,0T,
ξ3=0,2,1T,ξ4=5,-1,-3T,求A的对应于λ3的特征向量;
(Ⅲ)求矩阵A.
答案
参考答案:A~B.A,B有相同的秩和特征值.显然r(B)=1.B有特征值λ1=λ2=0且
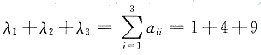 得λ3=14.故A有特征值λ1=λ2=0,λ3=14.
得λ3=14.故A有特征值λ1=λ2=0,λ3=14.
(Ⅱ)λ1=λ2=0是A的二重特征值,对应的线性无关特征向量最多有二个,由题设知η1=ξ1=1,1,0T,η2=ξ3=0,2,1T,线性无关,(取ξ1,ξ2,ξ3,ξ4,的极大线性无关组)故取η1=ξ1,η2=ξ3为λ=0的特征向量,因A是实对称阵,将λ3=14对应的特征向量设为η3=x1,x2,x3T,则η3与η1,η2正交,则有

即有
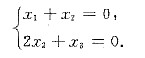
基础解系为η3=1,-1,2T,即是λ3=14对应的特征向量.
(Ⅲ)方法一 令P=η1,η2,η3,则
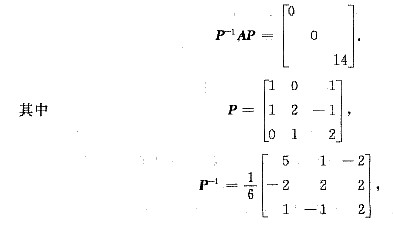
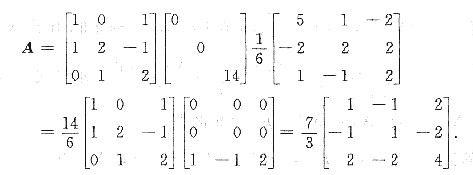
方法二 因与η3正交的非零向量均是A的对应于λ=0的特征向量,取一个与η1=ξ1=1,1,0T,η31,-1,2T.均正交的向量为η2,可得η2=1,-1,-1T.将η1,η2,η3单位化,并合并成正交阵,得

解析:[评注] 方法二用正交阵求A比用可逆阵求简单,且这里还没有利用施密特正交化方法.
