设α1,α2,…,αn是n个维列向量,已知齐次线性方程组
α1x1+α2x2+…+αnxn=0 (*)
只有零解,问齐次线性方程组
(α1+α2)x1+(α2+α3)x2+…+(αn-1+αn)xn-1+(αn+α1)xn=0(**)
是否有非零解若没有,说明理由;若有,求出方程组(**)的通解.
参考答案:齐次线性方程组
α1x1+α2x2+…+αnxn=0 (1)
只有零解,故其系数矩阵(记为A)的秩r(A)=rα1,α2,…,αn=n.
矩阵A是可逆方阵,齐次线性方程组
(α1+α2l+(α2+α3)x2+…+(αn-1+αn)xn-1+(αn+α1)xn=0 (2)
的系数矩阵(记为B)和A有如下关系:

当n=2k+1时,|C|=2≠0,故r(B)+r(c)=n,方程组(2)只有零解.
当n=2k时,|C|=0,故r(B)=r(c)<n,方程组(2)有非零解.
当n=2k时,B=AC,A可逆;故BX=0和CX=0是同解的方程组,故只需求解线性齐次方程组CX=0即可:对C作初等行变换,i行的-1倍加到i+1行,i=1,2,…,n-1.
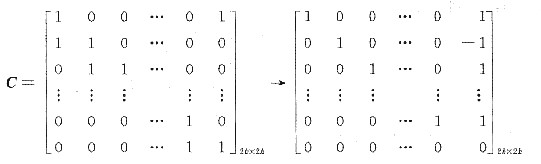
知r(B)=r(C)=2k-1,BX=0有一个非零向量ξ组成基础解系,且ξ=1,-1,1,…,1,-1T,故方程组(2)的通解为cξ=1,-1,1,…,1,-1T,其中c是任意常数.
或由C知,C中有n-1阶子式Cn-1,n-1≠0,故r(B)=r(C)=2k-1,BX=0有通解kξ,
由观察,因α1+α2-(α2+α3)+…-(α2k+α1)=0,
通解为k(1,-1,1,-1,…,-1),其中k是任意常数.
