解：猜想：在四面体P-ABC中，若三个侧棱PA，PB，PC 两两互相垂直，且三个侧面PAB，PBC，PAC分别与底面ABC所成的角为α，β，γ，则，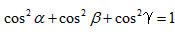

证明：如图，

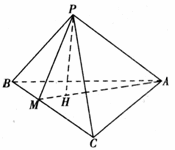
作PH⊥面ABC于H点，连接AH延长交BC于M点，

由PA与PB，PC垂直，可证明PA⊥面PBC，

所以PA⊥BC，

又PH⊥BC，

则BC⊥面PAH，

故AM⊥BC，PM⊥BC，则∠PMA为β，

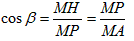
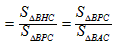
故，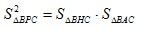

同理，可得，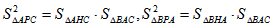

则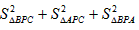

 ，

，，，

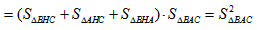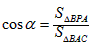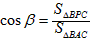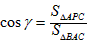=1。