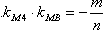问题
填空题
设A,B是圆x2+y2=r2上关于原点中心对称的两定点,M是圆周上异于A,B的动点且kMA,kMB存在,则kMA·kMB=-1,类比上述结论:设A,B是曲线mx2+ny2=1(m,n≠0,且m≠n)上关于原点中心对称的两定 点,M是曲线上异于A,B的动点且kMA,kMB存在,则:( )。
答案
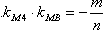
设A,B是圆x2+y2=r2上关于原点中心对称的两定点,M是圆周上异于A,B的动点且kMA,kMB存在,则kMA·kMB=-1,类比上述结论:设A,B是曲线mx2+ny2=1(m,n≠0,且m≠n)上关于原点中心对称的两定 点,M是曲线上异于A,B的动点且kMA,kMB存在,则:( )。