问题
填空题
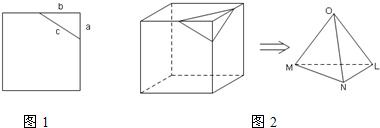
在平面上,用一条直线截正方形的一个角,截下的是一个直角三角形,有勾股定理c2=a2+b2,空间中的正方体,用一平面去截正方体的一角,截下的是三条侧棱两两垂直的三棱锥,三个两两垂直的侧面的面积分别为S1,S2,S3,截面面积为S,类比平面中的结论有______.
答案
建立从平面图形到空间图形的类比,
在由平面几何的性质类比推理空间立体几何性质时,我们常用的思路是:
由平面几何中点的性质,类比推理空间几何中线的性质;
由平面几何中线的性质,类比推理空间几何中面的性质;
由平面几何中面的性质,类比推理空间几何中体的性质;
三角形类比空间中的三棱锥,线段的长度类比图形的面积,
于是作出猜想:S2=S12+S22+S32
故答案为:S2=S12+S22+S32
