问题
单项选择题
在四边形ABCD中，设AB的长为8，∠A:∠B:∠C:∠D=3:7:4:10，∠CDB=60°，则△ABD的面积是（）。
A．8
B．32
C．4
D．16
答案
参考答案：D
解析：
由于四边形ABCD的4个内角之和为360°，
又∠A:∠B:∠C:∠D=3:7:4:10，而3+7+4+10=24，
故
又已知∠CDB=60°，则∠ADB=90°，故△ABD为等腰直角三角形，已知斜边AB=8，则高h=4，于是面积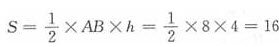
，故正确答案为D。
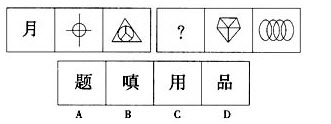