问题
问答题
某产品过去5年的销售额与目标市场人均收入的数据如表2-1所示，预计2007年该产品的目标市场人均收入为1800元。
表2-1 2000～2004年历年产品销售额与目标市场人均收入表
| 年份 | 2000 | 2001 | 2002 | 2003 | 2004 |
| 产品销售额(万元) | 30 | 35 | 36 | 38 | 40 |
| 人均收入(元) | 1000 | 1200 | 1250 | 1300 | 1400 |
问题：1．建立一元线性回归模型(参数计算结果小数点后保留3位)。
2．进行相关系数检验(取a＝0.05，只值小数点后保留3位，相关系数临界值见表2-2)。
3．对2007年可能的销售额进行点预测。
[*]
答案
参考答案：
解析：1．令y表示产品销售额，x表示目标市场人均收入。则一元线性回归模型为：
y=a+bx+e
根据已知数据，
∑xi＝1000+1200+1250+1300+1400＝6150
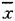=6150/5＝1230
∑yi=30+35+36+38+40＝179
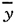＝179/5＝35.8
则 b=(222400-1230×179)/(7652500-1230×6150)＝0.025
a＝35.8-0.025×1230=5.05
则一元线性回归方程为：y＝5.05+0.025x+e
2．根据得到的一元线性回归方程，可得
y’1＝30.05；y’2＝35.05；y’3＝36.3；y’4＝37.55；y’5＝40.05；
则∑(yt-y’i)2＝0.3；∑(yi-)2＝56.8
因为R=0.997＞0.878
所以产品销售额和人均收入之间的线性关系成立。
3．2007年可能的销售额的点预测额为
y(2007)=5.05+0.025×1800＝50.05(万元)
