问题
填空题
在平面几何中有如下结论：正三角形ABC的内切圆面积为S1，外接圆面积为S2，则
|
答案
从平面图形类比空间图形，从二维类比三维，
可得如下结论：正四面体的外接球和内切球的半径之比是 3：1
故正四面体P-ABC的内切球体积为V1，外接球体积为V2之比等于
=(V1 V2
)3=1 3
．1 27
故答案为：
．1 27
搜题请搜索小程序“爱下问搜题”
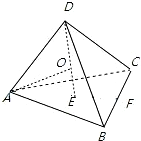
在平面几何中有如下结论：正三角形ABC的内切圆面积为S1，外接圆面积为S2，则
|
从平面图形类比空间图形，从二维类比三维，
可得如下结论：正四面体的外接球和内切球的半径之比是 3：1
故正四面体P-ABC的内切球体积为V1，外接球体积为V2之比等于
=(V1 V2
)3=1 3
．1 27
故答案为：
．1 27